Digital redlining

Back in the days American banks used to draw maps redlining the areas in which they don’t want to lend. Hence the term redlining.

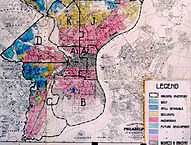“Home Owners’ Loan Corporation Philadelphia redlining map”. Licensed under Public Domain via Wikipedia

The problem was that those redlined neighbourhoods were typically populated by racial minorities. Even though banks were not using race information for denying credits directly, the policy was affecting racial minorities worse than others.

Digital redlining is the same but with algorithms. For example, nowadays banks are not allowed to use age in credit scoring models. So the first thing a bank decides is to remove the age variable from the inputs (true story).

All is fine if the other input variables are independent from age, but that’s rarely the case. Age may be correlated, for instance, with income. Income is a valid predictor for credit scoring, so it can be part of the model. What happens next?

If there was no age bias in the historical credit risk data then no problem. But if in there is an undesired age bias beyond what is explained by income, for instance, due to biased decisions in the past, then the credit scoring model would pick up those biases from the data even if age is removed from the model.

Here is a toy example. Suppose credit risk historically has been decided by human analysts presuming that younger clients have higher risk, and clients with lower income have higher risk. In the data income is related to age.

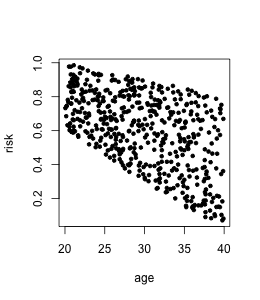
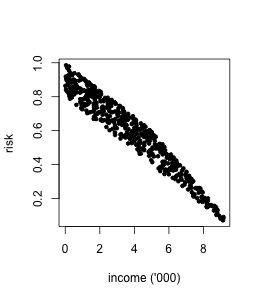
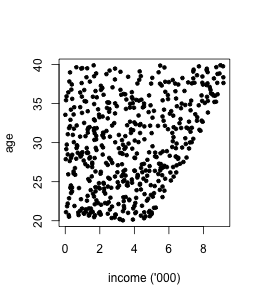
Now the bank is making a model for deciding upon credit risk automatically. If we fit a linear regression model on income and age, we get:

risk = -0.08*income - 0.01*age + 1.20.

Actually, the true model under which I generated the data is captured. But the age component is undesired and needs to be removed.

If age is removed from the data and a linear regression is learned, we get:

risk = -0.087*income + 0.930.

Not good. The coefficient at income is exaggerated, information about age is indirectly captured via income. Income serves as a digital red line.

Therefore, removing the protected characteristic is not enough, because that does not necessarily remove biases associated with it from decision making.