Braess's paradox

Braess’s paradox describes a situation in traffic planning, when adding an extra road makes things worse.

Suppose 4000 drivers want to get from sleeping place to work. There are two routes: first by train to station A, and then by car, or first by car to station B and then by train. The train trip takes 45 min, and the car trip takes N/100 min, where N is the number of cars taking this road.

Here is how it looks:

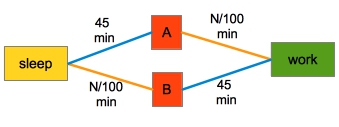
Assuming that drivers know the current traffic situation, the equilibrium would settle at half of the drivers (2000) going route A, and the other half route B. For each driver the trip would take 45+20 = 65 min.

Now imagine the local government decides to build a bridge between A and B. Assume crossing the bridge takes 0 time. Now everybody (4000 drivers) would go by car following the orange route.

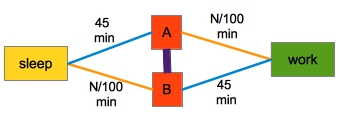
The trip would take 40+40 = 80 min, which is by 15 min longer than before. However, nobody would switch to train, since that would take even longer (45+45=90min). Traveling one leg by train would also take longer (40+45=85min). So, everybody is worse-off due to the bridge.